2021 AMC 12B 试题/第1题
题目
有多少个整数值的 \( x \) 满足 \( \left| x\right| < {3\pi } \) ?
(A) 9 (B) 10 (C) 18 (D) 19 (E) 20
解法1
由于 \( {3\pi } \) 约为9.42,我们将9乘以2以计入1到9以及-1到-9的数,并加1以计入0,得到 \( \sigma \) (D) 19 sparty101 并由 Tony_Li2007 编辑
解法2
\( \left| x\right| < {3\pi } \Leftrightarrow - {3\pi } < x < {3\pi } \) 。由于 \( \pi \) 约为3.14, \( {3\pi } \) 约为9.42。我们要求解 \( - {9.42} < x < {9.42} \) ,其中 \( x \in \mathbb{Z} \) 。因此, \( - {9.42} < x < {9.42} \Rightarrow - 9 \leq x \leq 9 \) ,对于 \( x \in \mathbb{Z} \) 。 \( x \) 的整数值个数为 \( 9 - \left( {-9}\right) + 1 = {19} \) 。因此,答案是 \( \left| {\left( \mathbf{D}\right) {19}}\right| \) ~ \{TSun\} ~
解法3
\( {3\pi } \approx {9.4} \) 。这里有两种情况。
当 \( x > 0,\left| x\right| > 0 \) ,且 \( x = \left| x\right| \) 。于是 \( x < {9.4} \)
当 \( x < 0,\left| x\right| > 0, \) 且 \( x = - \left| x\right| . \) 于是 \( - x < {9.4} \) 。除以-1并翻转符号,我们得到 \( x > - {9.4}. \) 由情况1和2可知 \( - {9.4} < x < {9.4} \) 。由于 \( x \) 是整数, \( x \) 必须在-9到9之间。总共有
\[ 9 - \left( {-9}\right) + 1 = 0\left( {D - {19}}\right) \text{integers.} \]
-PureSwag
解法4
观察题目,我们发现它并未直接说 \( x \) ,而是 \( \left| x\right| . \) 这意味着 \( x \) 的所有可能值既有正也有负。将 \( \pi \) 四舍五入到3得到 \( 3\left( 3\right) = 9 \) 。有9个正解和9个负解。 \( 9 + 9 = {18} \) 。但零呢?尽管零既非负也非正,我们仍需将其计入解中,因此答案是 \( 9 + 9 + 1 = {18} + 1 = 0 \) 。D。
2021 AMC 10B 试题/第2题
问题
\( \sqrt{{\left( 3 - 2\sqrt{3}\right) }^{2}} + \sqrt{{\left( 3 + 2\sqrt{3}\right) }^{2}} \) 的值是多少?
(A) 0 (B) \( 4\sqrt{3} - 6 \) (C) 6 (D) \( 4\sqrt{3} \) (E) \( 4\sqrt{3} + 6 \)
解答
注意,任何平方的平方根总是该平方数的绝对值,因为平方根函数只返回正数。将3和 \( 2\sqrt{3} \) 平方后,我们发现 \( 2\sqrt{3} > 3 \) ,因此 \( 3 - 2\sqrt{3} \) 为负,故需取 \( 3 - 2\sqrt{3} \) 的绝对值,即 \( 2\sqrt{3} - 3 \) 。由此,表达式中的第一项等于 \( 2\sqrt{3} - 3 \) ,第二项为 \( 3 + 2\sqrt{3} \) ,两者相加得 \( \mid \left( \mathbf{D}\right) 4\sqrt{3} \) 。
~bjc, abhinavg0627 和 JackBocresion
解答 2
设 \( x = \sqrt{{\left( 3 - 2\sqrt{3}\right) }^{2}} + \sqrt{{\left( 3 + 2\sqrt{3}\right) }^{2}} \) ,则 \( {x}^{2} = {\left( 3 - 2\sqrt{3}\right) }^{2} + 2\sqrt{{\left( -3\right) }^{2}} + {\left( 3 + 2\sqrt{3}\right) }^{2} \) 。 \( 2\sqrt{{\left( -3\right) }^{2}} \) 项源于平方差公式。化简表达式得 \( {x}^{2} = {48} \) ,因此 \( x = {16} \) , \( 4\sqrt{3} \) ~ shrungpatel
2021 AMC 10B 试题/第3题
问题
在一项面向高二和高三学生的课后项目中,辩论队由来自两个年级且人数相等的学生组成。在项目的28名学生中, \( {25}\% \) 的高二学生和 \( {10}\% \) 的高三学生加入了辩论队。问项目中有多少名高二学生?
(A) 5 (B) 6 (C) 8 (D) 11 (E) 20
解答 1
设项目中有 \( j \) 名高二学生和 \( s \) 名高三学生。将百分比化为分数, \( \frac{j}{4} \) 和 \( \frac{s}{10} \) 在辩论队中,且由于高二与高三在辩论队的人数相等, \( \frac{j}{4} = \frac{s}{10} \) 。
交叉相乘并化简得 \( {5j} = {2s}. \) 。此外,项目共有28名学生, \( j + s = {28}. \) 。现在只需解方程组
\[ {5j} = {2s} \]
\[ j + s = {28}, \]
解得 \( j = 8, s = {20} \) 。由于我们要求的是高二学生人数,答案为
-纯酷
解法2(快速但不严谨)
我们立刻看出 \( E \) 是唯一可能的高年级人数,因为 \( {10}\% \) 只能对应以0结尾的选项。因此高年级人数为20,低年级人数为 \( {28} - {20} = 8 \rightarrow C \) 。~samrocksnature
解法3
由于辩论队中低年级与高年级人数相等,假设有 \( x \) 名低年级和 \( x \) 名高年级。该人数分别占低年级的 \( {25}\% = \frac{1}{4} \) 和高年级的 \( {10}\% = \frac{1}{10} \) ,由此可知共有 \( {4x} \) 名低年级和 \( {10x} \) 名高年级。整个项目共有28名低年级与高年级学生,因此得到
\[ {10x} + {4x} = {28}, \]
\[ {14x} = {28}, \]
\[ x = 2\text{.} \]
这意味着辩论队中有 \( {4x} = 8 \) 名低年级学生, \( \mathrm{\left( C\right) 8} \)
解法4(排除法)
低年级人数必须是4的倍数,因为恰好 \( \frac{1}{4} \) 的学生在辩论队。因此,我们立即看出 \( C \) 和 \( E \) 是低年级人数仅有的两种可能。然而,若有20名低年级,则高年级为8人,此时 \( 1/{10} \) 的高年级在辩论队并不成立,因为 \( \frac{1}{10} \cdot 8 = \frac{4}{5} \) 不是整数。于是,我们得出低年级有8人,故答案为 \( C \)
2021 AMC 12B 第2题
以下题目同时出现在2021 AMC 10B第4题和2021 AMC 12B第2题,因此两题均重定向至此页。
题目
在一次数学竞赛中,57名学生穿蓝色衬衫,另有75名学生穿黄色衬衫。这132名学生被分成66对。其中恰好有23对的两名学生都穿蓝色衬衫。有多少对的两名学生都穿黄色衬衫?
(A) 23 (B) 32 (C) 37 (D) 41 (E) 64
解答
有46名学生与穿蓝色衬衫的搭档配对。其余11名穿蓝色衬衫的学生必须与穿相反颜色衬衫的搭档配对。还剩下64名学生。因此所求的对数为
\( \frac{64}{2} = \) (B) 32 土拨鼠菲尔
2021年AMC 10B试题/第5题
问题
乔妮的四个堂兄妹的年龄是互不相同的个位正整数。其中两人的年龄相乘得24,另外两人的年龄相乘得30。求乔妮这四个堂兄妹的年龄之和。
(A) 21 (B) 22 (C) 23 (D) 24 (E) 25
解决方案
首先看两位表亲的年龄相乘等于24。由于年龄必须是单个数字,年龄只能是3和8或4和6。
接下来,看看两位表亲的年龄相乘等于30的情况。由于年龄必须是个位数,唯一可能的年龄是5和6。记住所有年龄必须各不相同,唯一可行的解是年龄分别为3、8和5、6。
我们需要求出年龄的总和,即
\[ 3 + 8 + 5 + 6 = {(B}){22}. \]
2021年AMC 12B试题/第4题
以下题目同时出现在2021年AMC 10B第6题和2021年AMC 12B第4题,因此两道题均重定向至此页面。
问题
布莱克韦尔女士给两个班级进行了一场考试。上午班学生的平均分为84分,下午班的平均分为70分。上午班学生人数与下午班学生人数之比
班级是 \( \frac{3}{4} \) 。所有学生成绩的平均值是多少?
(A) 74 (B) 75 (C) 76 (D) 77 (E) 78
解决方案 1
不妨设上午班有3名学生,下午班有4名学生,则平均分为 \( \frac{3 \cdot {84} + 4 \cdot {70}}{7} = \) (C)76
解决方案 2
设上午班有 \( {3x} \) 名学生,下午班有 \( {4x} \) 名学生。学生总数为 \( {3x} + {4x} = {7x} \) 。平均值为 \( \frac{{3x} \cdot {84} + {4x} \cdot {70}}{7x} = {76} \) 。因此,答案是 \( \frac{\left( \mathrm{C}\right) {76}}{7x} \) 。
\[ \sim \{ \text{TSun}\} \sim \]
解法3(双变量)
假设上午班有 \( m \) 名学生,下午班有 \( a \) 名学生。我们有以下图表:
| 学生人数 | 均值 | 总计 | |
| 上午 | \( m \) | 84 | 84m |
| 下午 | \( a \) | 70 | 70a |
我们还已知 \( \frac{m}{a} = \frac{3}{4} \) ,可整理为 \( m = \frac{3}{4}a \) 。
所有学生得分的平均值为
\[ \frac{{84m} + {70a}}{m + a} = \frac{{84}\left( {\frac{3}{4}a}\right) + {70a}}{\frac{3}{4}a + a} = \frac{133a}{\frac{7}{4}a} = {133} \cdot \frac{4}{7} = 6\text{.} \]
~MRENTHUSIASM
解法4(比例)
在平均值中, \( \frac{3}{3 + 4} = \frac{3}{7} \) 的分数来自上午班, \( \frac{4}{7} \) 的分数来自下午班。平均值为 \( \frac{3}{7} \cdot {84} + \frac{4}{7} \cdot {70} = 1 \) (C)76
~Kinglogic
2021 AMC 10B 试题/第7题
题目
在平面上,四个半径分别为1、3、5、7的圆均与直线 \( \ell \) 在同一点 \( A, \) 相切,但它们可以位于 \( \ell \) 的任一侧。区域 \( S \) 由恰好位于这四个圆中一个圆内的所有点组成。区域 \( S \) 的最大可能面积是多少?
(A) \( {24\pi } \) (B) \( {32\pi } \) (C) \( {64\pi } \) (D) \( {65\pi } \) (E) \( {84\pi } \)
解法1
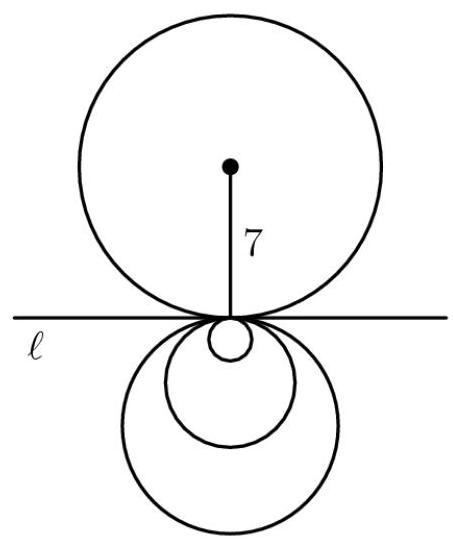
经过一些愿望式思考和观察,我们发现上述配置使面积最大化,面积为 \( {49\pi } + \left( {{25} - 9}\right) \pi = {65\pi } \rightarrow \left( \mathbf{D}\right) \)
- samrocksnature
- 不失一般性,我们将半径为7的圆画在 \( \ell \) 的北侧。
- 为了使所求区域面积最大化,我们凭直觉画一个半径为5的圆,使其位于 \( \ell \) 的南侧。
- 现在,我们至少需要减去一个半径为3的圆。最优情形是半径为3的圆完全包含半径为1的圆,这样就不必再减去更多区域。也就是说,两个最小的圆位于 \( \ell , \) 的同一侧,但可以在任一侧。解法1中的图示给出了四个圆的一种可能位置。
解法2(用直觉解释解法1)
假设每个圆位于直线 \( \ell \) 的北侧或南侧。我们逐个构造这些圆:
综上,答案为 \( {7}^{2}\pi + {5}^{2}\pi - {3}^{2}\pi = 0 \) (D) \( {65\pi } \)
2021 AMC 10B 试题/第8题
题目
周先生将1到225的所有整数填入一个15×15的方格。他把1放在正中间的格子(第8行第8列),然后按顺时针方向依次填入其余数字,如下方部分图示所示。问:最上面第二行中出现的最大数与最小数之和是多少?
| ... | ... | ... | ... | ... | ... | ... |
| ... | 21 | 22 | 23 | 24 | 25 | ... |
| ... | 20 | 7 | 8 | 9 | 10 | ... |
| ... | 19 | 6 | 1 | 2 | 11 | ... |
| ... | 18 | 5 | 4 | 3 | 12 | ... |
| ... | 17 | 16 | 15 | 14 | 13 | ... |
| ... | ... | ... | ... | ... | ... | ... |
\( \textbf{(A)}{367}\;\textbf{(B)}{368}\;\textbf{(C)}{369}\;\textbf{(D)}{379}\;\textbf{(E)}{380} \)
解决方案 1
通过观察可知,正方形的右上角始终是一个平方数,因此15×15网格的右上角为225。减去14可得左上角为211。同理可求出左下角和右下角的值。接着,由于第二行的边长比首行少一格,我们从右上角减去13即可得到最右侧格子的值。类似地,可求出第二行从左数第二格的值是157。由此可知,第二行的最小数为157,最大数为其左侧一格,比211小1。将157与210相加得到 \( \left( \mathbf{A}\right) {367} \)
-Dynosol(Dynosol)
解法2:画出来
画出图示后,我们得到 \( \Delta \mathbf{A} \) (A)367。请注意,这主要用于验证你的答案。
~塔可12
解法3(解法1与解法2的图示)
在下面的两种解法中,请注意黄色单元格中的数字是连续的奇完全平方数(consecutive odd perfect squares)。我们可以通过归纳法证明这一点。
从这里开始有两种图示解法。
解法3.1(解法1的示例——仅考虑5个方格)
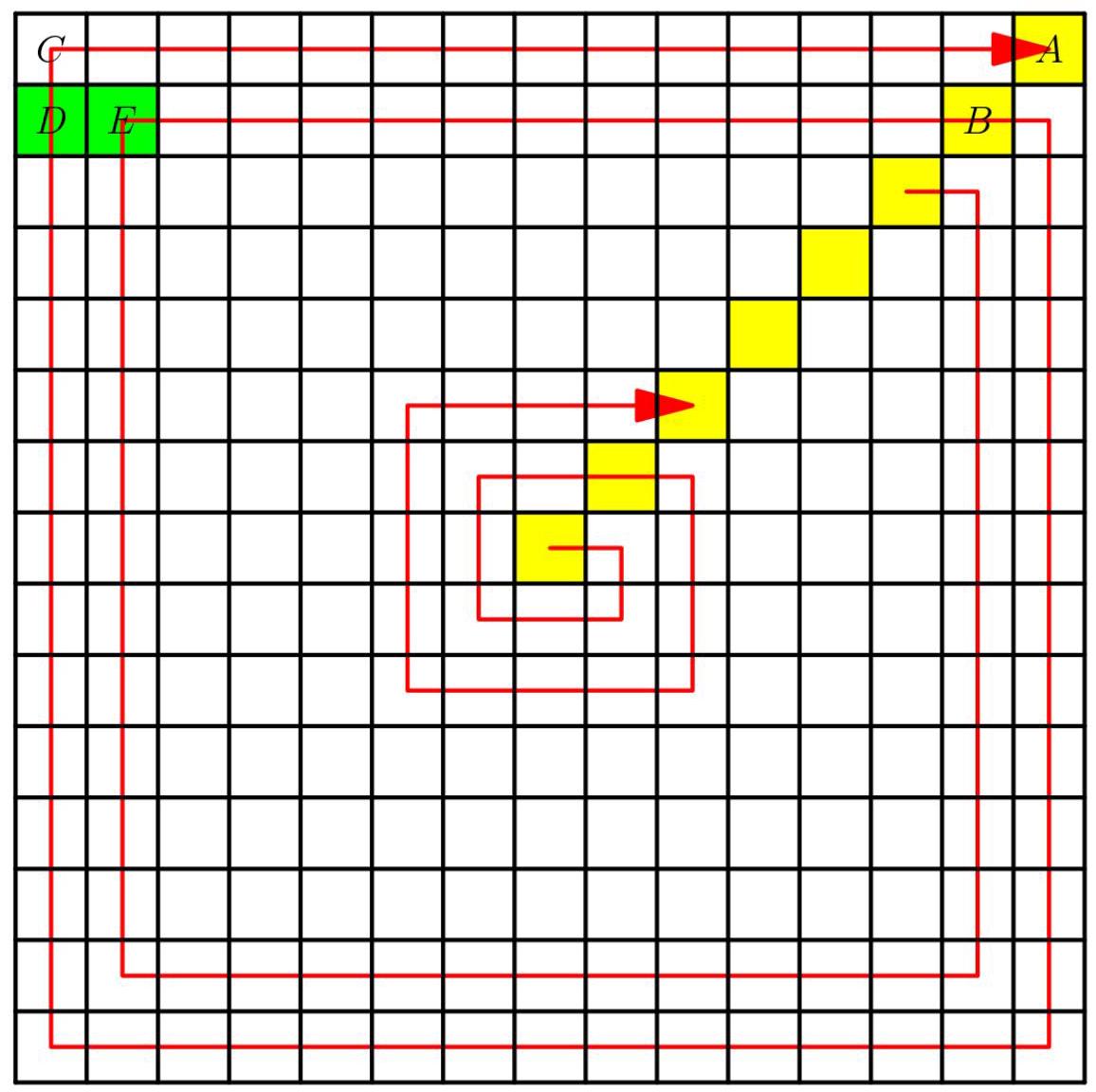
在上图中,红色箭头表示数字的递增方向。从上往下第二行中,最大数和最小数分别为 \( D \) 和 \( E, \) 。通过观察,我们按如下步骤进行:
\[ A = {15}^{2} = {225},\;B = {13}^{2} = {169}\; \Rightarrow \;C = - A - {14} = - {211} \]
\[ \Rightarrow \;D = C - 1\; = \;{210} \]
\[ \Rightarrow E = B - {12} = {157} \]
因此,答案是 \( D + E = \epsilon \) ,367。
~热情
解法3.2(解法2的图示——绘制全部225个方格)
| 211 | 212 | 213 | 214 | 215 | 216 | 217 | 218 | 219 | 220 | 221 | 222 | 223 | 224 | 225 |
| 210 | 157 | 158 | 159 | 160 | 161 | 162 | 163 | 164 | 165 | 166 | 167 | 168 | 169 | 170 |
| 209 | 156 | 111 | 112 | 113 | 114 | 115 | 116 | 117 | 118 | 119 | 120 | 121 | 122 | 171 |
| 208 | 155 | 110 | 73 | 74 | 75 | 76 | 77 | 78 | 79 | 80 | 81 | 82 | 123 | 172 |
| 207 | 154 | 109 | 72 | 43 | 44 | 45 | 46 | 47 | 48 | 49 | 50 | 83 | 124 | 173 |
| 206 | 153 | 108 | 71 | 42 | 21 | 22 | 23 | 24 | 25 | 26 | 51 | 84 | 125 | 174 |
| 205 | 152 | 107 | 70 | 41 | 20 | 7 | 8 | 9 | 10 | 27 | 52 | 85 | 126 | 175 |
| 204 | 151 | 106 | 69 | 40 | 19 | 6 | 1 | 2 | 11 | 28 | 53 | 86 | 127 | 176 |
| 203 | 150 | 105 | 68 | 39 | 18 | 5 | 4 | 3 | 12 | 29 | 54 | 87 | 128 | 177 |
| 202 | 149 | 104 | 67 | 38 | 17 | 16 | 15 | 14 | 13 | 30 | 55 | 88 | 129 | 178 |
| 201 | 148 | 103 | 66 | 37 | 36 | 35 | 34 | 33 | 32 | 31 | 56 | 89 | 130 | 179 |
| 200 | 147 | 102 | 65 | 64 | 63 | 62 | 61 | 60 | 59 | 58 | 57 | 90 | 131 | 180 |
| 199 | 146 | 101 | 100 | 99 | 98 | 97 | 96 | 95 | 94 | 93 | 92 | 91 | 132 | 181 |
| 198 | 145 | 144 | 143 | 142 | 141 | 140 | 139 | 138 | 137 | 136 | 135 | 134 | 133 | 182 |
| 197 | 196 | 195 | 194 | 193 | 192 | 191 | 190 | 189 | 188 | 187 | 186 | 185 | 184 | 183 |
根据上方的完整图示,答案为 \( {210} + {157} = (\mathbf{A} \) )367。
2021年AMC 12B试题/第5题
以下题目同时出现在2021年AMC 10B第9题和2021年AMC 12B第5题,因此两道题均重定向至此页面。
问题
点 \( P\left( {a, b}\right) \) 在 \( {xy} \) -平面内先绕点(1,5)逆时针旋转 \( {90}^{ \circ } \) ,再关于直线 \( y = - x \) 作反射。经过这两次变换后, \( P \) 的像位于(-6,3)。求 \( b - a \) 。
(A) 1 (B) 3 (C) 5 (D) 7 (E) 9
解决方案
\( P \) 的最终像为(-6,3)。我们知道关于 \( y = - x \) 的反射规则是 \( \left( {x, y}\right) - - > \left( {-y, - x}\right) \) ,因此在反射之前、旋转之后该点的坐标为(-3,6)。
根据旋转的定义,(-3,6)与(1,5)之间的斜率必须与(a, b)与(1,5)之间的斜率垂直。第一个斜率为 \( \frac{5 - 6}{1 - \left( {-3}\right) } = \frac{-1}{4} \) 。这意味着 \( P \) 与(1,5)的斜率为4。
旋转同样保持到旋转中心的距离不变,既然我们仅“沿斜率”上下一次就从(3, -6)到达(1,5),那么从(1,5)到 \( P \) 也只需使用一次斜率即可。
因此点 \( P \) 位于 \( \left( {1 + 1,5 + 4}\right) = \left( {2,9}\right) \) 。答案是 \( 9 - 2 = 7 = \) (D)
2021年AMC 12B试题/第6题
以下题目同时出现在2021年AMC 10B第10题和2021年AMC 12B第6题,因此两道题均重定向至此页面。
问题
一个倒置的圆锥,底面半径为 \( {12}\mathrm{{cm}} \) ,高为 \( {18}\mathrm{{cm}} \) ,内部装满水。将这些水全部倒入一个高圆柱体中,该圆柱体的水平底面半径为 \( {24}\mathrm{{cm}} \) 。求圆柱体内水的高度(厘米)。
(A) 1.5 (B) 3 (C) 4 (D) 4.5 (E) 6
解法1
圆锥的体积为 \( \frac{1}{3} \cdot \pi \cdot {r}^{2} \cdot h \) ,其中 \( r \) 为底面半径, \( h \) 为高。水完全填满圆锥,因此水的体积为 \( \frac{1}{3} \cdot {18} \cdot {144\pi } = 6 \cdot {144\pi } \) 。
圆柱的体积为 \( \pi \cdot {r}^{2} \cdot h \) ,因此水在圆柱中的体积为 \( {24} \cdot {24} \cdot \pi \cdot h \) 。
由于水的体积不变,可将两式相等: \( {24} \cdot {24} \cdot \pi \cdot h = 6 \cdot {144\pi } \) 。我们得到 \( {4h} = 6 \) 和 \( h = \frac{6}{4}. \) 。
因此答案为 \( {1.5} = \) (A)
-abhinavg0627
解法2(比例法)
水完全填满圆锥。先假设圆锥与圆柱的半径相同,则圆锥的体积是圆柱的 \( \frac{1}{3} \) ,因此高度需除以3。根据题意,半径加倍,意味着底面积变为原来的4倍(因为 \( {2}^{2} = 4 \) )。
因此,高度先除以3再除以4,结果为 \( {18} \div 3 \div 4 = {1.5} = \) (A)
2021 AMC 10B 试题/第11题
题目
奶奶刚烤好一大矩形盘的布朗尼。她打算用平行于盘边的直线将其切成大小形状相同的矩形小块,每刀必须贯穿整个盘。奶奶希望内部块数与边缘块数相同。她最多能切出多少块布朗尼?
(A) 24 (B) 30 (C) 48 (D) 60 (E) 64
解法1
设矩形盘边长为 \( m \) 和 \( n \) 。由于一半的布朗尼块位于内部,可得 \( \left( {m - 2}\right) \left( {n - 2}\right) = \frac{mn}{2} \) 。于是 \( 2\left( {m - 2}\right) \left( {n - 2}\right) = {mn} \Leftrightarrow {mn} - {4m} - 4\overline{n} + 8 = 0 \) 。两边加8并应用西蒙最爱因式分解技巧,得到 \( \left( {m - 4}\right) \left( {n - 4}\right) = 8 \) 。由于 \( m \) 和 \( n \) 均为正,可得 \( \left( {m, n}\right) = \left( {5,{12}}\right) ,\left( {6,8}\right) \) (顺序可互换)。经检验, \( 5 \cdot {12} = \) (D) 60使布朗尼数量最大。
~ ike.chen
解决方案 2
显然,矩形烤盘的任何一边都不能少于5块布朗尼。我们让烤盘的一边恰好有5块布朗尼,并设其邻边有 \( x \) 块布朗尼。因此, \( {5x} = 2 \cdot 3\left( {x - 2}\right) \) ,解得 \( x = {12} \) ,于是烤盘中共有 \( 5 \cdot {12} = {60} \) 块布朗尼。64是唯一大于60的选项,但它不可能是答案,因为要让64块布朗尼排成烤盘且任何一边都不少于5块,只能排成每边8块的正方形,而这不符合题意。因此,答案是 \( \begin{array}{l} \text{ (D) }{60} \\ \end{array} \)
2021年AMC 12B试题/第7题
以下题目同时出现在2021年AMC 10B第12题和2021年AMC 12B第7题,因此两道题均重定向至此页面。
问题
设 \( N = {34} \cdot {34} \cdot {63} \cdot {270} \) 。求 \( N \) 的所有奇数除数之和与所有偶数除数之和的比值。
(A) \( 1 : {16} \) (B) \( 1 : {15} \) (C) \( 1 : {14} \) (D) \( 1 : 8 \) (E) \( 1 : 3 \)
解决方案 1
将 \( N \) 进行质因数分解(prime factorize)得到 \( N = {2}^{3} \cdot {3}^{5} \cdot 5 \cdot 7 \cdot {17}^{2} \) 。对于 \( N \) 的每个奇数因子(odd divisor) \( n \) ,都存在 \( N \) 的偶数因子(even divisors) \( {2n},{4n},{8n} \) ,因此比值为 \( 1 : \left( {2 + 4 + 8}\right) \rightarrow \) (C)。
解决方案 2
对 \( N \) 进行质因数分解(prime factorizing),我们得到 \( N = {2}^{3} \cdot {3}^{5} \cdot 5 \cdot 7 \cdot {17}^{2} \) 。 \( N \) 的所有奇因数(odd divisors)之和等于不含因子2的所有因数之和;而所有偶因数(even divisors)之和等于总因数之和减去奇因数之和。奇因数之和由下式给出
\[ a = \left( {1 + 3 + {3}^{2} + {3}^{3} + {3}^{4} + {3}^{5}}\right) \left( {1 + 5}\right) \left( {1 + 7}\right) \left( {1 + {17} + {17}^{2}}\right) \]
且所有除数之和为
\[ \left( {1 + 2 + 4 + 8}\right) \left( {1 + 3 + {3}^{2} + {3}^{3} + {3}^{4} + {3}^{5}}\right) \left( {1 + 5}\right) \left( {1 + 7}\right) \left( {1 + {17} + {17}^{2}}\right) = {15a} \]
因此,我们的比率为
\[ \frac{a}{{15a} - a} = \frac{a}{14a} = \frac{1}{14} \]
2021年AMC 10B试题/第13题
问题
设 \( n \) 为正整数, \( d \) 为数字,使得在 \( n \) 进制下,数字 \( \underline{32d} \) 的值为263,且 \( \underline{324} \) 在 \( n \) 进制下的值等于 \( \underline{11}\underline{d}\underline{1} \) 在六进制下的值。 \( n + d \) 是多少?
(A) 10 (B) 11 (C) 13 (D) 15 (E) 16
解法
我们可以先建立一个方程,把 \( \underline{32d} \) 从 \( n \) 进制转换为十进制。转换后得到 \( 3{n}^{2} + {2n} + d \) 。因为它等于263,所以可将该方程设为263。最后,两边同时减去 \( d \) ,得到 \( 3{n}^{2} + {2n} = {263} - d \) 。
我们也可以建立方程,把 \( \underline{324} \) 从 \( n \) 进制和 \( \underline{11}\underline{d1} \) 从6进制转换为十进制。把 \( \underline{324} \) 转换为十进制的方程是 \( 3{n}^{2} + {2n} + 4 \) 。把 \( \underline{11d1} \) 从6进制转换为十进制的方程是 \( {6}^{3} + {6}^{2} + {6d} + 1 \) 。
化简 \( {6}^{3} + {6}^{2} + {6d} + 1 \) 得到 \( {6d} + {253}. \) 。将上述两个方程设为相等,我们有
\[ 3{n}^{2} + {2n} + 4 = {6d} + {253}. \]
两边同时减去4,得到 \( 3{n}^{2} + {2n} = {6d} + {249} \) 。
然后我们可以使用方程
\[ 3{n}^{2} + {2n} = {263} - d \]
\[ 3{n}^{2} + {2n} = {6d} + {249} \]
来解 \( d \) 。令 \( {263} - d \) 等于 \( {6d} + {249} \) 并求解,得到 \( d = 2 \) 。
将 \( d = 2 \) 代回方程 \( 3{n}^{2} + {2n} = {263} - d \) 。两边同时减去261,得到最终方程 \( 3{n}^{2} + {2n} - {261} = 0 \) 。用二次公式求解,得到解为9和-10。因为进制必须为正,所以 \( n = 9 \) 。
9加2得到 \( \sigma 8{11}\sigma \)
-Zeusthemoose(为可读性编辑)
解法2
当两者都按十进制解释时, \( {32d} \) 大于263,因此 \( n \) 小于10。通过尝试可得 \( n = 9 \) 。263在9进制下为322,所以答案是 \( 9 + 2 = \left( \text{B}\right) {11} \)
2021 AMC 12B 试题/第8题
以下题目同时出现在2021 AMC 10B第14题和2021 AMC 12B第8题,因此两题均重定向至此页面。
题目
三条等距平行线与一圆相交,形成三条长度分别为38、38和34的弦。求相邻两条平行线之间的距离。
(A) \( 5\frac{1}{2} \) (B) 6 (C) \( 6\frac{1}{2} \) (D) 7 (E) \( 7\frac{1}{2} \)
方案1
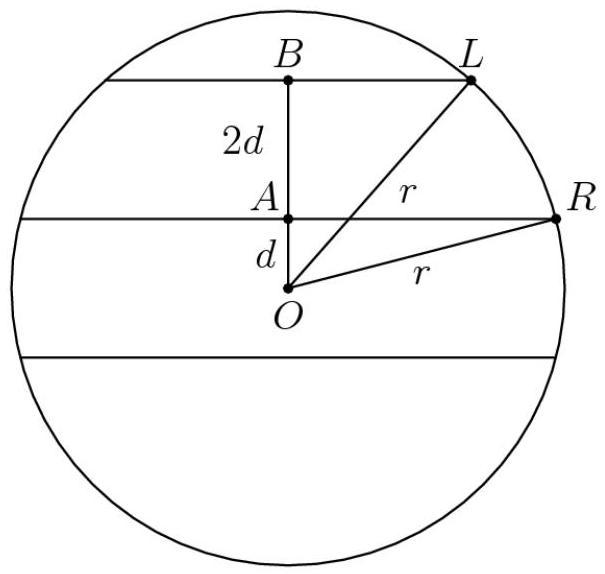
由于两条平行弦长度相等(均为38),它们到圆心的距离必然相等。设每条弦到圆心的垂直距离为 \( d \) 。因此,长度为34的弦到圆心的距离为
\[ {2d} + d = {3d} \]
各弦之间的距离仅为 \( {2d} \) 。设圆的半径为 \( r \) 。从圆心向直线与圆的交点作半径,可得到两个不同的直角三角形:
- 一个底边为 \( \frac{38}{2} = {19} \) 、高为 \( d \) 、斜边为 \( r \) (图中标记为 \( \bigtriangleup {RAO} \) )的三角形
- 另一个的底边为 \( \frac{34}{2} = {17} \) ,高为 \( {2d} + d \) ,斜边为 \( r \) (图中标记为 \( \bigtriangleup {LBO} \) )
根据毕达哥拉斯定理(Pythagorean theorem),我们可以建立如下方程组:
\[ {19}^{2} + {d}^{2} = {r}^{2} \]
\[ {17}^{2} + {\left( 2d + d\right) }^{2} = {r}^{2} \]
求解,我们得到 \( d = 3 \) ,因此 \( {2d} = 456 \)
-由Joeya提供的解答,由Jamess2022(burntTacos)绘制的示意图。(若有人能修正该示意图,请帮忙。——已修正。)
解法2(坐标法)
因为我们知道圆的方程为 \( {\left( x - a\right) }^{2} + {\left( y - b\right) }^{2} = {r}^{2} \) ,其中圆心为(a, b),半径为 \( r \) ,所以我们可以把圆心放在原点来求出这个圆的方程。这样做后,我们得到方程为 \( {x}^{2} + {y}^{2} = {r}^{2} \) 。现在,我们可以把两弦之间的距离设为 \( {2d} \) ,于是长度为38的弦到直径的距离就是 \( d \) 。
因此,下列各点位于圆上;由于y轴将弦平分,我们由此得到x值:
(19, d)
(19, - d)
(17, - 3d)
现在,我们可以将前两个值中的一个以及最后一个值代入,得到以下方程:
\[ {19}^{2} + {d}^{2} = {r}^{2} \]
\[ {17}^{2} + {\left( 3d\right) }^{2} = {r}^{2} \]
将这两个方程相减,我们得到 \( {19}^{2} - {17}^{2} = 8{d}^{2} \) ——因此,我们得到 \( {72} = \underline{8{d}^{2}} \rightarrow {d}^{2} = 9 \rightarrow d = 3 \) 。我们想求 \( {2d} = 6 \) ,因为它就是两条弦之间的距离。所以,答案是 \( B \) 。
2021年AMC 10B试题/第15题
问题
实数 \( x \) 满足方程 \( x + \frac{1}{x} = \sqrt{5} \) ,求 \( {x}^{11} - 7{x}^{7} + {x}^{3} \) 的值。
(A) -1 (B) 0 (C) 1 (D) 2 (E) \( \sqrt{5} \)
解法1
我们将 \( x + \frac{1}{x} = \sqrt{5} \) 平方得到 \( {x}^{2} + 2 + \frac{1}{{x}^{2}} = 5 \) 。两边减去2得到 \( {x}^{2} + \frac{1}{{x}^{2}} = 3 \) ,再平方一次,发现 \( {x}^{4} + 2 + \frac{1}{{x}^{4}} = 9 \) ,因此 \( {x}^{4} + \frac{1}{{x}^{4}} = 7 \) 。将原式 \( {x}^{11} - 7{x}^{7} + {x}^{3} \) 除以 \( {x}^{7} \) ,可得它等于 \( {x}^{7}\left( {{x}^{4} - 7 + \frac{1}{{x}^{4}}}\right) \) 。于是,因为 \( {x}^{4} + \frac{1}{{x}^{4}} \) 为7,所以等于 \( {x}^{7}\left( 0\right) = 0 \) 。
解法2
两边同乘 \( x \) 并用二次公式,得到 \( \frac{\sqrt{5} \pm 1}{2} \) 。可设其为 \( \frac{\sqrt{5} + 1}{2} \) ,并注意到这也是方程 \( {x}^{2} - x - 1 = 0 \) 的解,即我们有 \( {x}^{2} = x + 1 \) 。反复应用此关系(也可直接观察斐波那契数列),
\[ \left( {x}^{11}\right) - 7{x}^{7} + {x}^{3} = \left( {{x}^{10} + {x}^{9}}\right) - 7{x}^{7} + {x}^{3} \]
\[ = \left( {2{x}^{9} + {x}^{8}}\right) - 7{x}^{7} + {x}^{3} \]
\[ = \left( {3{x}^{8} + 2{x}^{7}}\right) - 7{x}^{7} + {x}^{3} \]
\[ = \left( {3{x}^{8} - 5{x}^{7}}\right) + {x}^{3} \]
\[ = \left( {-2{x}^{7} + 3{x}^{6}}\right) + {x}^{3} \]
\[ = \left( {{x}^{6} - 2{x}^{5}}\right) + {x}^{3} \]
\[ = \left( {-{x}^{5} + {x}^{4} + {x}^{3}}\right) \]
\[ = - {x}^{3}\left( {{x}^{2} - x - 1}\right) = 0 \]
~LCZ
解法3
我们立即注意到 \( {x}^{11} - 7{x}^{7} + {x}^{3} \) 的指数构成等差数列,因此它们关于中间项对称。于是 \( {x}^{11} - 7{x}^{7} + {x}^{3} = {x}^{7}\left( {{x}^{4} - 7 + \frac{1}{{x}^{4}}}\right) \) 。由于 \( x + \frac{1}{x} = \sqrt{5} \) , \( {x}^{2} + 2 + \frac{1}{{x}^{2}} = 5 \) ,因此 \( {x}^{2} + \frac{1}{{x}^{2}} = 3 \) 。继续下去,得到 \( {x}^{4} + 2 + \frac{1}{{x}^{4}} = 9 \) ,所以 \( {x}^{4} - 7 + \frac{1}{{x}^{4}} = 0 \) 。我们甚至不需要求出 \( {x}^{3} \) !因为 \( {x}^{3} \cdot 0 \) 显然为0,这就是答案~sosiaops
解法4
首先将 \( x + \frac{1}{x} = \sqrt{5} \) 乘以 \( x \) ,得到 \( {x}^{2} + 1 = \sqrt{5}x \) 。现在看到方程: \( {x}^{11} - 7{x}^{7} + {x}^{3} \) 。各项都有 \( {x}^{3} \) ,可将其提出,于是所求变为 \( {x}^{3}\left( {{x}^{8} - 7{x}^{4} + 1}\right) \) 。观察
回到我们最初的方程,我们有 \( {x}^{2} + 1 = \sqrt{5}x \) ,它等于 \( {x}^{2} = \sqrt{5}x - 1 \) 。利用这一点,我们可以计算 \( {x}^{4} \) https://artofproblemsolving.com/wiki/index.php/2021_AMC_10B_Problems/Problem_15 Art of Problem Solving 得到 \( 5{x}^{2} - 2\sqrt{5}x + 1 \) ,并且我们发现还有另一个 \( {x}^{2} \) ,于是我们再次代入,得到 \( 3\sqrt{5}x - 4 \) 。用同样的方法,我们得到 \( {x}^{8} \) 等于 \( {11}\sqrt{5}x - {29} \) 。我们把它代入 \( {x}^{3}\left( {{x}^{8} - 7{x}^{4} + 1}\right) \) ,得到 \( {x}^{3}\left( 0\right) \) ,所以答案是(B) 0
2021 AMC 10B 问题/第16题
题目
若一个正整数的每一位数字都严格大于前一位数字,则称其为上坡整数。例如,1357、89和5都是上坡整数,而32、1240和466则不是。有多少个上坡整数能被15整除?
(A) 4 (B) 5 (C) 6 (D) 7 (E) 8
解法1
15的整除规则是:该数必须模3同余0且模5同余0。能被5整除意味着末位必须是5或0。我们可以立即排除末位为0的情况,因为唯一一个“上坡”且末位为0的整数是0,而0不是正数。因此,该数末位必为5。观察选项,答案都很小,于是我们可以列出所有“上坡”且能被3整除的数:15、45、135、345、1245、12345,共6个数,选C。
解法2
首先注意,为了被15整除,该数末位必须是5或0。然而末位不能为0,因为0不大于前面的任何数字。因此末位必为5。按位数分情况讨论。情况1:1位数。无解,0个。情况2:2位数。有15、45、75,但75不是上坡数,故2个。情况3:3位数。有135、345,共2个。情况4:4位数。有1235、1245、2345,但只有1245满足条件,故1个。情况5:5位数。只有12345,1个。合计 \( 2 + 2 + 1 + 1 = 6 \) 。C ~JustinLee2017
解法3
与解法2类似,我们按情况讨论。一个数能被15整除当且仅当它能被3和5整除。此时个位必须是5,否则无法构成满足条件的数。
情况1:数字和 \( = 6 \)
只有15一个数。
情况2:数字和 \( = 9 \)
有两个数:45和135。
情况3:数字和 \( = {12} \)
有两个数:345和1245。
情况4:数字和=15
只有12345一个数。
可见所有情况已穷尽,因为若数字和更大,则需使用大于5的数字,从而破坏题设条件。答案为 \( \mathbf{\left( C\right) } \) 。
~coolmath34
解法4(按删除12345各位数字的情况分类讨论)
对于每一个正整数:
- 它能被3整除当且仅当其数字和能被3整除。
- 它能被5整除当且仅当其个位数字为0或5。
https://artofproblemsolving.com/wiki/index.php/2021_AMC_10B_Problems/Problem_16
\( \bullet \) 它能被15整除当且仅当它同时能被3和5整除。
由于所求正整数为递增数,其个位数字必须为5。我们从最大的这种递增整数(经观察为12345)开始,然后按删除其各位数字的情况进行分类讨论。显然,我们不能删除数字5,因为这是满足被5整除规则的唯一方式。现在,我们关注被3整除的规则。
注意,被删除数字的和必须是3的倍数,这样 \( 1 + 2 + 3 + 4 + 5 = {15} \) 与该和的差也能被3整除(快速证明:假设被删除数字的和为 \( {3k} \) ,则 \( {15} - {3k} = 3\left( {5 - k}\right) \) 必须能被3整除)。由此得到两种解法:
解法4.1(按删除数字的个数分类讨论)
情况(1):恰好删除0个数字。(5位递增整数)此情况下有1个递增整数:12345。情况(2):恰好删除1个数字。(4位递增整数)我们只能删除数字3。因此,此情况下有1个递增整数:1245。情况(3):恰好删除2个数字。(3位递增整数)我们只能删除和为3或6的数字。因此,此情况下有2个递增整数:345,135。情况(4):恰好删除3个数字。(2位递增整数)我们只能删除和为6或9的数字。因此,此情况下有2个递增整数:45,15。总计:我们的答案是 \( 1 + 1 + 2 + 2 = 0 \) (C) 6。~MRENTHUSIASM
解法4.2(按被删除数字的和分类讨论)
情况(1):被删除数字的和为0。(剩余数字的和为15。)
此情况下有1个递增整数:12345。
情况(2):被删除数字的和为3。(剩余数字的和为12。)
注意 \( 3 = 1 + 2. \) 因此,此情况下有2个递增整数:1245,345。
情况(3):被删除数字的和为6。(剩余数字的和为9。)
注意 \( 6 = 2 + 4 = 1 + 2 + 3. \) 因此,此情况下有2个递增整数:135,45。
情况(4):被删去的数字之和为9。(剩余数字之和为6。)
注意 \( 9 = 2 + 3 + 4. \) 因此,本情况有1个上坡整数:15。
总计
综上,我们的答案是 \( 1 + 2 + 2 + 1 = \) (C) 6。
2021 AMC 10B 试题/第17题
题目
拉冯、奥斯卡、阿迪蒂、泰隆和金一起玩纸牌游戏。每人从编号为 \( 1,2,3,\ldots ,{10}. \) 的10张牌中各得2张。玩家的得分为其两张牌数字之和。各玩家得分如下:拉冯-11,奥斯卡-4,阿迪蒂-7,泰隆-16,金-17。以下哪项陈述为真?
(A) 拉冯拿到了牌3。
(B) 阿迪蒂拿到了牌3。
(C) 拉冯拿到了牌4。
(D) 阿迪蒂拿到了牌4。
(E) 泰隆拿到了牌7。
解法1
奥斯卡必拿到3和1,因此排除(A)和(B)。若泰隆拿到7,则他还需拿到9,于是金必须拿到10和7,从而排除 \( \left( \underline{\mathbf{E}}\right) \) 。若阿迪蒂拿到4,则她还需拿到3,而3已被奥斯卡拿走。故答案为(C)拉冯拿到了牌4。
~smarty101 与 smartypantsno_3
解法2
奥斯卡必须拿到3和1。阿蒂蒂不能拿3或1,因此她必须拿2和5。同理,雷文不能拿1、2、3或5,所以他必须拿4和7,答案是(C) 雷文拿到了牌4。
-SmileKat32
解法3(全面但非必要)
通过观察,我们按分数从低到高考虑。我们做出如下逻辑推断:
奥斯卡的分数是4。 \( \Rightarrow \) 奥斯卡拿到了牌1和3。
\( \Rightarrow \) 阿蒂蒂拿到了牌2和5。
\( \Rightarrow \) 雷文拿到了牌4和7。
\( \Rightarrow \) 泰隆拿到了牌6和10。
\( \Rightarrow \) 金拿到了牌8和9。
因此,答案是(C) 雷文拿到了牌4。
当然,如果我们更早查看选项,那么在该逻辑陈述块的第3行后就可以停止。
2021 AMC 10B 第18题
题目
一枚公平的6面骰子被反复掷出,直到出现奇数为止。求在首次出现奇数之前,每个偶数都至少出现一次的概率。
(A) \( \frac{1}{120} \) (B) \( \frac{1}{32} \) (C) \( \frac{1}{20} \) (D) \( \frac{3}{20} \) (E) \( \frac{1}{6} \)
解法1
我们选出的第一个数字为偶数的概率为 \( \frac{3}{6} \) 。
下一个与第一个数字不同的数字为偶数的概率为 \( \frac{2}{5} \) 。
再下一个与前两个数字都不同的数字为偶数的概率为 \( \frac{1}{4} \) 。
\( \frac{3}{6} \cdot \frac{2}{5} \cdot \frac{1}{4} = \frac{1}{20} \) ,因此答案为 \( \left( {\mathbf{C})\frac{1}{20}}\right) \) 。
~Tucker
解法2
从 \( \{ 1,2,3,4,5,6\} \) 中任取的三元组成为最先出现的3个不同数字的概率均等。
因此,最先出现的3个不同数字为 \( \{ 2,4,6\} \) 的概率为 \( \frac{1}{\left( \begin{array}{l} 6 \\ 3 \end{array}\right) } = C \cdot \frac{1}{20} \) 。
~kingofpineapplz
解法3(速解)
注意,本题实质是求在1,2,3,4,5,6的某个排列中,前三个位置恰好都是偶数的概率。
6个数字共有 \( 6! \) 种排列方式,其中前三个位置为偶数、后三个位置为奇数的排列有 \( 3!\left( {3!}\right) \) 种。
因此概率为 \( \frac{3!\left( {3!}\right) }{6!} = \frac{1}{20} = \) (C)。
-abhinavg0627
解法4
设 \( {P}_{n} \) 表示第一个奇数在第 \( n \) 次掷出且满足所有条件的概率。接下来我们使用补集计数法。
对于 \( n \leq 3 \) ,不可能让全部3个偶数都出现在一个奇数之前。请注意,对于 \( n \geq 4, \)
\[ {P}_{n} = \frac{1}{{2}^{n}} - \frac{1}{{2}^{n}}\left( \frac{\left( \begin{array}{l} 3 \\ 2 \end{array}\right) \left( {{2}^{n - 1} - 2}\right) + \left( \begin{array}{l} 3 \\ 2 \end{array}\right) }{{3}^{n - 1}}\right) = \frac{1}{{2}^{n}} - \left( \frac{3\left( {2}^{n - 1}\right) - 3}{{2}^{n} \cdot {3}^{n - 1}}\right) = \frac{1}{{2}^{n}} - \left( {\frac{1}{2 \cdot {3}^{n - 2}} - \frac{1}{{2}^{n} \cdot {3}^{n - 2}}}\right) \]
对所有 \( n \) 求和,我们得到答案https://artofproblemsolving.com/wiki/index.php/2021_AMC_10B_Problems/Problem_18
\[ \left( {\frac{1}{{2}^{4}} + \frac{1}{{2}^{5}} + \ldots }\right) - \left( {\frac{1}{2 \cdot {3}^{2}} + \frac{1}{2 \cdot {3}^{3}} + \ldots }\right) + \left( {\frac{1}{{2}^{4} \cdot {3}^{2}} + \frac{1}{{2}^{5} \cdot {3}^{3}} + \ldots }\right) = \left( \frac{1}{8}\right) - \left( \frac{\frac{1}{18}}{\frac{2}{3}}\right) + \left( \frac{\frac{1}{14}}{\frac{5}{6}}\right) = \left( \frac{1}{8}\right) - \left( \frac{1}{12}\right) + \left( \frac{1}{120}\right) = 1\text{(C)}\frac{1}{20}\text{.} \]
~ike.chen
解决方案5
设 \( {E}_{n} \) 为在还需要 \( n \) 个不同偶数的情况下,问题条件被满足的概率,则
\[ {E}_{1} = \frac{1}{6} + \frac{1}{3} \cdot {E}_{1} + \frac{1}{2} \cdot 0, \]
由于存在 \( \frac{1}{3} \) 的概率会掷出已经出现过的偶数,我们将再次回到相同的状态。求解后,我们得到 \( {E}_{1} = \frac{1}{4} \) 。
我们可以将相同的概念应用于 \( {E}_{2} \) 和 \( {E}_{3} \) 。我们发现
\[ {E}_{2} = \frac{1}{3} \cdot {E}_{1} + \frac{1}{6} \cdot {E}_{2} + \frac{1}{2} \cdot 0, \]
因此 \( {E}_{2} = \frac{1}{10} \) 。此外,
\[ {E}_{3} = \frac{1}{2} \cdot {E}_{2} + \frac{1}{2} \cdot 0 \]
所以 \( {E}_{3} = \frac{1}{20} \) 。由于题目要求 \( {E}_{3} \) ,我们的答案是 \( 1\mathrm{C}2\frac{1}{20} \) 。-BorealBear
解法6(与解法1相同,但稍作补充说明)
第一次抽到偶数的概率是 \( \frac{1}{2} \) ;既然已经抽到了,它就不再影响后续问题,因此即使再次抽到该数,对我们的问题也无关紧要。现在,在剩下的5个数中,再抽到偶数的概率是5;同样,抽到这个数后,它也被排除在外。此时只剩4个数,抽到最后一个偶数的概率是 \( \frac{1}{4} \) ,所以答案是
\[ \frac{1}{2} \times \frac{2}{5} \times \frac{1}{4} = \frac{1}{20} \]
2021年AMC 12B试题/第12题
以下题目同时出现在2021年AMC 10B第19题和2021年AMC 12B第12题,因此两道题均重定向至此页面。
问题
设 \( S \) 是一个由正整数构成的有限集合。若将 \( S \) 中的最大整数移除,则剩余整数的平均值(算术平均数)为32。若再将最小整数也移除,则剩余整数的平均值为35。若随后将最大整数放回集合,则整数的平均值升至40。原集合 \( S \) 中的最大整数比最小整数大72。求集合 \( S \) 中所有整数的平均值。
(A) 36.2 (B) 36.4 (C) 36.6 (D) 36.8 (E) 37 解法1
设 \( x \) 为最大整数, \( y \) 为最小整数, \( z \) 为集合S中除去 \( x \) 和 \( y \) 后所有数的和, \( k \) 为集合S的元素个数。
于是, \( S = x + y + z \)
首先,当移除最大整数时, \( \frac{S - x}{k - 1} = {32} \)
当最小整数也被移除时, \( \frac{S - x - y}{k - 2} = {35} \)
当把最大整数加回来时, \( \frac{S - y}{k - 1} = {40} \)
已知 \( x = y + {72} \)
代入 \( x = y + {72} \) 后,你得到含3个未知数 \( S \) 、 \( y \) 和 \( k \) 的3个方程。
\[ S - y - {72} = {32k} - {32} \]
\[ S - {2y} - {72} = {35k} - {70} \]
\[ S - y = {40k} - {40} \]
这很容易解出 \( k = {10} \) 、 \( y = 8 \) 、 \( S = {368} \) 。
\( \therefore \) 集合 \( = S/k = {368}/{10} = {36.8} \) 中所有整数的平均值,D)
~ SoySoy4444
解法2
我们代入36.2,并假设除35部分外其余都成立。接着计算该部分得到35.75。我们还发现,根据代入时使用的公式,当增加0.2时,35.75部分减少0.25。于是答案就是 \( D \) 36.8。因为是选择题,可以倒推,无需深入思考。
2021 AMC 12B 试题/第15题
以下题目同时出现在2021 AMC 10B第20题和2021 AMC 12B第15题,因此两题均重定向至此页。
题目
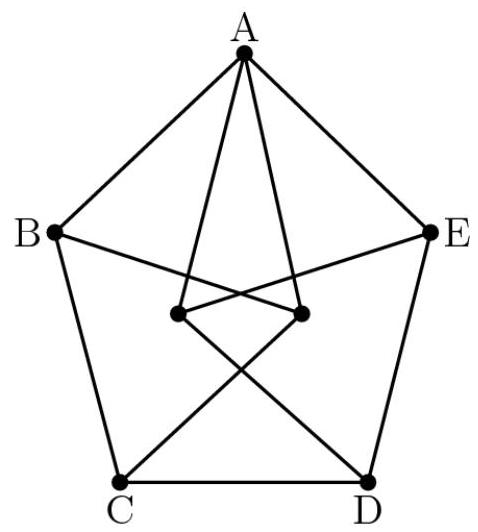
该图形由11条线段构成,每条线段长度为2。五边形 \( {ABCDE} \) 的面积可表示为 \( \sqrt{m} + \sqrt{n} \) ,其中 \( m \) 和 \( n \) 为正整数。 \( m + n \) 是多少?
(A) 20 (B) 21 (C) 22 (D) 23 (E) 24
解法1
设 \( M \) 为 \( {CD} \) 的中点。注意到由于等边三角形的存在, \( {AED} \) 和 \( {ABC} \) 都是 \( {120} - {30} - {30} \) 三角形,因此 \( {AM} = \sqrt{A{D}^{2} - M{D}^{2}} = \sqrt{{12} - 1} = \sqrt{11} \Longrightarrow \left\lbrack {ACD}\right\rbrack = \sqrt{11} \) 。同时,
\( \left\lbrack {AED}\right\rbrack = 2 \cdot 2 \cdot \frac{1}{2} \cdot \sin {120}^{o} = \sqrt{3} \) ,所以
\( \left\lbrack {ABCDE}\right\rbrack = \left\lbrack {ACD}\right\rbrack + 2\left\lbrack {AED}\right\rbrack = \sqrt{11} + 2\sqrt{3} = \sqrt{11} + \sqrt{12} \Rightarrow \) (D) 23
解法2
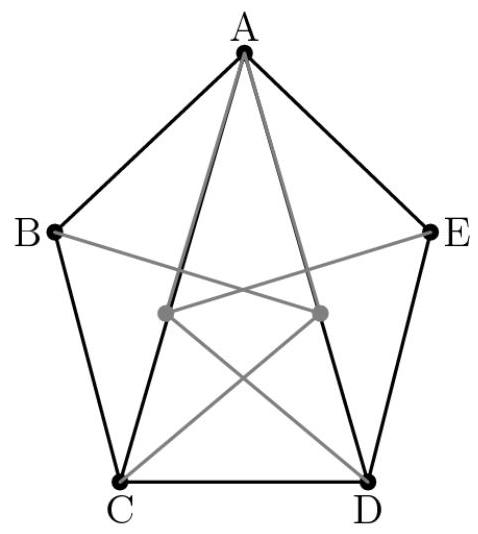
作对角线 \( {AC} \) 和 \( {AD} \) ,将五边形分成三部分。我们可以分别计算每个三角形的面积,最后求和。对于三角形 \( {ABC} \) 和 \( {ADE} \) ,它们各自的面积为 \( 2 \cdot \frac{1}{2} \cdot \frac{4\sqrt{3}}{4} = \sqrt{3} \) 。对于三角形 \( {ACD} \) ,可以看出 \( {AC} = {AD} = 2\sqrt{3} \) 和 \( {CD} = 2 \) 。利用勾股定理,该三角形的高为 \( \sqrt{11} \) ,因此面积为 \( \sqrt{11} \)
2021 AMC 10B 试题/第21题
题目
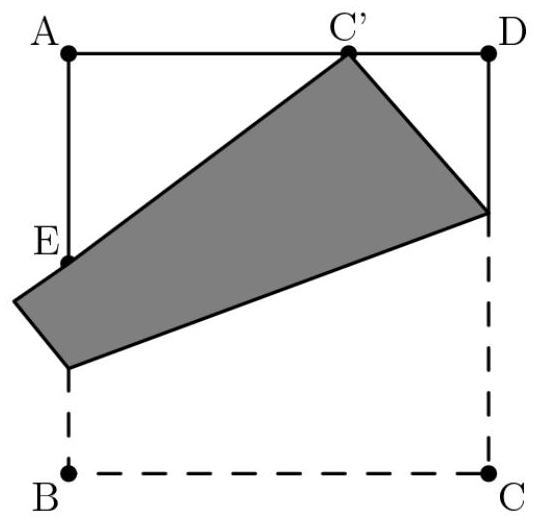
一张正方形纸片边长为1,顶点依次为 \( A, B, C, \) 和 \( D \) 。如图所示,将纸片折叠,使顶点 \( C \) 落在边 \( \overline{AD} \) 上的点 \( {C}^{\prime } \) ,且边 \( \overline{BC} \) 与边 \( \overline{AB} \) 相交于点 \( E \) 。已知 \( {C}^{\prime }D = \frac{1}{3} \) 。求三角形 \( \bigtriangleup {AE}{C}^{\prime } \) 的周长?
(A) 2 (B) \( 1 + \frac{2}{3}\sqrt{3} \) (C) \( \sqrt{136} \) (D) \( 1 + \frac{3}{4}\sqrt{3} \) (E) \( \frac{7}{3} \)
解法1
设折叠发生在 \( {CD} \) 上的点为 \( F \) 。令 \( {FD} \) 为 \( x \) , \( {CF} \) 为 \( 1 - x \) ,由于折叠对称。可识别出这是一个直角三角形,解 \( x \) 得:
\[ {x}^{2} + {\left( \frac{1}{3}\right) }^{2} = {\left( 1 - x\right) }^{2} \rightarrow {x}^{2} + \frac{1}{9} = {x}^{2} - {2x} + 1 \rightarrow x = \frac{4}{9} \]
我们知道这是一个3-4-5三角形,因为边长为 \( \frac{3}{9},\frac{4}{9},\frac{5}{9} \) 。又 \( {EA}{C}^{\prime } \) 与 \( {C}^{\prime }{DF} \) 相似,因为角 \( {C}^{\prime } \) 是直角。现在可用相似性得出周长即为 \( {C}^{\prime }{DF} * \frac{A{C}^{\prime }}{DF} \) 的周长。
那正是 \( \frac{4}{3} * \frac{\frac{2}{3}}{\frac{4}{9}} = \frac{4}{3} * \frac{3}{2} = 2 \) 。因此最终答案为 \( A \)
~Tony_Li2007
解法2
设我们要反射的直线为 \( \ell \) ,设它与 \( {AB} \) 和 \( {CD} \) 的交点分别为 \( M \) 和 \( N \) 。注意,对一条直线作反射时,我们需找到一条过两对称点中点(即反射点与原像点)的垂线。因此,我们先求直线 \( \ell \) 的方程。线段 \( C{C}^{\prime } \) 的斜率为 \( \frac{0 - 1}{1 - 2/3} = - 3 \) ,这意味着直线 \( \ell \) 的斜率为 \( \frac{1}{3} \) 。此外,
线段 \( C{C}^{\prime } \) 的中点为 \( \left( {\frac{5}{6},\frac{1}{2}}\right) \) ,因此直线 \( \ell \) 经过该点。于是,直线 \( \ell \) 的方程即为 \( y = \frac{1}{3}x + \frac{2}{9} \) 。若点 \( B \) 关于直线 \( \ell \) 的反射点为 \( {B}^{\prime } \) ,则 \( B{B}^{\prime } \) 就是直线 \( y = - {3x} \) 。直线 \( \ell \) 与线段 \( B{B}^{\prime } \) 的交点为 \( \left( {-\frac{1}{15},\frac{1}{5}}\right) \) 。于是,我们得到 \( {B}^{\prime } = \left( {-\frac{2}{15},\frac{2}{5}}\right) \) 。接着,线段 \( {B}^{\prime }{C}^{\prime } \) 的方程为 \( y = \frac{3}{4}x + \frac{1}{2} \) ,因此点 \( E \) 是 \( y \) -截距,即 \( \left( {0,\frac{1}{2}}\right) \) 。这意味着 \( {AE} = \frac{1}{2}, A{C}^{\prime } = \frac{2}{3} \) ,根据勾股定理(Pythagorean Theorem), \( E{C}^{\prime } = \frac{5}{6} \) (或者你也可以注意到 \( \bigtriangleup {AE}{C}^{\prime } \) 是一个 \( 3 - 4 - 5 \) 的直角三角形)。于是,周长为 \( \frac{1}{2} + \frac{2}{3} + \frac{5}{6} = 2 \) ,所以答案为 \( \left( {\text{A) }2}\right) \) 。-rocketsr
解法3(伪解):
假设E是 \( \overline{AB} \) 的中点,则 \( \overline{AE} = \frac{1}{2} \) ,且由于 \( {C}^{\prime }D = \frac{1}{3} \) , \( \overline{A{C}^{\prime }} = \frac{2}{3} \) 。根据勾股定理(Pythagorean Theorem), \( \overline{E{C}^{\prime }} = \frac{5}{6} \) 。易得所求周长为 \( 2 \rightarrow A \) -samrocksnature
解法4
如解法1所述,我们可以发现 \( {DF} = \frac{4}{9} \) ,且 \( {C}^{\prime }F = \frac{5}{9} \) 。接着,通过用 \( {AE} \) 以两种方式表示 \( \overline{EF} \) 的长度,我们可以求出 \( \overline{AE} \) 的长度。若设 \( {AE} = a \) ,根据勾股定理(Pythagorean Theorem)可得 \( {EC} = \sqrt{{a}^{2} + {\left( \frac{2}{3}\right) }^{2}} = \sqrt{{a}^{2} + \frac{4}{9}} \) 。因此,既然已知 \( \angle E{C}^{\prime }F \) 为直角,再次运用勾股定理可得 \( {EF} = \sqrt{{\left( \sqrt{{a}^{2} + \frac{4}{9}}\right) }^{2} + {\left( \frac{5}{9}\right) }^{2}} = \sqrt{{a}^{2} + \frac{61}{81}} \) 。表达 \( {EF} \) 的另一种方法是对 \( \bigtriangleup {XEF} \) 使用勾股定理,其中 \( X \) 为从 \( F \) 到 \( \overline{AE} \) 的垂足。我们注意到 \( {ADFX} \) 是一个矩形,因此可知 \( {AD} = 1 = {FX} \) 。其次,由于
\( {FD} = \frac{4}{9},{EX} = a - \frac{4}{9} \) 因此,通过勾股定理(Pythagorean Theorem),我们得出
\( {EF} = \sqrt{{\left( a - \frac{4}{9}\right) }^{2} + {1}^{2}} = \sqrt{{a}^{2} - \frac{8}{9}a + \frac{97}{81}}. \)
既然我们已经为同一长度找到了两个表达式,就得到了方程 \( \sqrt{{a}^{2} + \frac{61}{81}} = \sqrt{{a}^{2} - \frac{8}{9}a + \frac{97}{81}} \) 。
解之,我们得到 \( a = \frac{1}{2} \) 。
最后,我们看到 \( \bigtriangleup {AE}{C}^{\prime } \) 的周长是 \( \frac{1}{2} + \frac{2}{3} + \sqrt{{\left( \frac{1}{2}\right) }^{2} + \frac{4}{9}} \) ,可以化简为2。因此,答案是 \( \left( A\right) 2 \) 。Jaffytaffy
2021年AMC 10B试题/第22题
问题
Ang、Ben 和 Jasmin 每人各有 5 块积木,颜色分别为红、蓝、黄、白、绿;另有 5 个空盒子。三人各自独立且随机地将手中每块积木放入一个盒子。求至少有一个盒子收到
3个同色方块的概率为 \( \frac{m}{n} \) ,其中 \( m \) 和 \( n \) 为互质的正整数。 \( m + n \) 的值是多少?
(A) 47 (B) 94 (C) 227 (D) 471 (E) 542
解决方案 1
令我们的分母为 \( {\left( 5!\right) }^{3} \) ,因此我们考虑所有可能的分布。
我们使用容斥原理(Principle of Inclusion and Exclusion,PIE)来计算成功的数量。
当我们有一个at1box(盒子)且该盒中all3balls(全部3个球)颜色相同时,共有 \( {}_{5}{C}_{1}{ \cdot }_{5}{P}_{1} \cdot {\left( 4!\right) }^{3} \) 种分配方式( \( {C}_{1} \) 种从五个盒子中选择一个盒子使其颜色统一, \( {}_{5}{P}_{1} \) 种为该盒子选择颜色, \( 4! \) 种让三人各自放置剩余物品)。
然而,我们重复计算了那些有两个盒子颜色一致的分布情况,共有 \( {}_{5}{C}_{2}{ \cdot }_{5}{P}_{2} \cdot {\left( 3!\right) }^{3} \) 种这样的分布方式(从五个盒子中选出两个设为统一颜色有5 \( {C}_{2} \) 种方法,为这两个盒子选择颜色有5 \( {P}_{2} \) 种方法,剩下的三个物品由三人各自放置各有 \( 3! \) 种方法)。
再次,我们需要把三个颜色一致的盒子重新加回分布中……依此类推。
根据容斥原理(PIE),我们的成功计数为
\[ {}_{5}{C}_{1}{ \cdot }_{5}{P}_{1} \cdot {\left( 4!\right) }^{3} - {}_{5}{C}_{2}{ \cdot }_{5}{P}_{2} \cdot {\left( 3!\right) }^{3} + {}_{5}{C}_{3}{ \cdot }_{5}{P}_{3} \cdot {\left( 2!\right) }^{3} - {}_{5}{C}_{4}{ \cdot }_{5}{P}_{4} \cdot {\left( 1!\right) }^{3} + {}_{5}{C}_{5}{ \cdot }_{5}{P}_{5} \cdot {\left( 0!\right) }^{3} = {120} \cdot {2556}. \]
\[ \frac{{120} \cdot {2556}}{{120}^{3}} = \frac{71}{400} \]
得到答案 \( {471}\left( D\right) \)
解法2
与解法1相同,概率为
\[ \frac{{(\frac{5}{1})} \cdot 5 \cdot (4!{)}^{3} - {(\frac{5}{2})} \cdot 5 \cdot 4 \cdot (3!{)}^{3} + {(\frac{5}{3})} \cdot 5 \cdot 4 \cdot 3 \cdot (2!{)}^{3} - {(\frac{5}{4})} \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot (1!{)}^{3} + {(\frac{5}{5})} \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{(5!{)}^{3}} \]
\[ = \frac{5 \cdot 5 \cdot {\left( 4!\right) }^{3} - {10} \cdot 5 \cdot 4 \cdot {\left( 3!\right) }^{3} + {10} \cdot 5 \cdot 4 \cdot 3 \cdot {\left( 2!\right) }^{3} - 5 \cdot 5! + 5!}{{\left( 5!\right) }^{3}}. \]
除以 \( 5! \) ,我们得到
\[ \frac{5 \cdot {\left( 4!\right) }^{2} - {10} \cdot {\left( 3!\right) }^{2} + {10} \cdot {\left( 2!\right) }^{2} - 5 + 1}{{\left( 5!\right) }^{2}}\text{.} \]
除以4,我们得到
\[ \frac{5 \cdot 6 \cdot {24} - {10} \cdot 9 + {10} - 1}{{30} \cdot {120}}. \]
除以9,我们得到
\[ \frac{5 \cdot 2 \cdot 8 - {10} + 1}{{10} \cdot {40}} = \frac{71}{400} \Rightarrow \text{ (D) }{471} \]
解法3
解题的艺术
使用补集计数。记 \( {T}_{n} \) 为3个人将 \( n \) 种颜色分配到 \( n \) 个盒子的总方式数,其中 \( {f}_{n} \) 种方式满足没有任何盒子颜色一致。注意 \( {T}_{n} = {\left( n!\right) }^{3} \) 。由此设定可见,题目要求的是 \( 1 - \frac{{f}_{5}}{{\left( 5!\right) }^{3}} \) 。为求 \( {f}_{5} \) ,我们需要排除以下情况:a) 1个盒子颜色一致;b) 2个盒子颜色一致;c) 3个盒子颜色一致;d) 4个盒子颜色一致;e) 5个盒子颜色一致。情况d)与e)重合。于是我们有
\[ {f}_{5} = {T}_{5} - \left( \begin{array}{l} 5 \\ 1 \end{array}\right) \left( \begin{array}{l} 5 \\ 1 \end{array}\right) \cdot {f}_{4} - \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \cdot 2! \cdot {f}_{3} - \left( \begin{array}{l} 5 \\ 3 \end{array}\right) \left( \begin{array}{l} 5 \\ 3 \end{array}\right) \cdot 3! \cdot {f}_{2} - 5! \]
在情况b)中,有 \( \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \) 种方式选择2个颜色一致的盒子, \( \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \) 种方式选择两种颜色,2!种方式排列选定的两种颜色,以及 \( {f}_{3} \) 种方式使剩余3个盒子颜色不一致。情况a)和c)同理。在情况e)中,5种颜色的全排列共有5!种方式。现在,我们只需计算 \( {f}_{2},{f}_{3} \) 和 \( {f}_{4} \) 。
我们有 \( {f}_{2} = {T}_{2} - 2 = {\left( 2!\right) }^{3} - 2 = 6 \) ,因为我们减去了盒子颜色一致的方案数,即2。
同理, \( {f}_{3} = {T}_{3} - \left\lbrack {3! + \left( \begin{array}{l} 3 \\ 1 \end{array}\right) \left( \begin{array}{l} 3 \\ 1 \end{array}\right) \cdot {f}_{2}}\right\rbrack = {156} \) ——再次,我们必须减去至少1个盒子颜色一致的方案数。若3个盒子各自颜色一致,有 \( 3! \) 种方式;2个盒子各自颜色一致与之前相同。若仅1个盒子颜色一致,有 \( \left( \begin{array}{l} 3 \\ 1 \end{array}\right) \) 种方式选择该盒子, \( \left( \begin{array}{l} 3 \\ 1 \end{array}\right) \) 种方式为其选择颜色,1!种方式排列选定的颜色,以及 \( {f}_{2} \) 种方式使剩余2个盒子颜色不一致。类似地,
\[ {f}_{4} = {\left( 4!\right) }^{3} - \left\lbrack {4! + \left( \begin{array}{l} 4 \\ 2 \end{array}\right) \left( \begin{array}{l} 4 \\ 2 \end{array}\right) \cdot 2! \cdot {f}_{2} + \left( \begin{array}{l} 4 \\ 1 \end{array}\right) \left( \begin{array}{l} 4 \\ 1 \end{array}\right) \cdot {f}_{3}}\right\rbrack = {10},{872} \]
因此,
\[ {f}_{5} = {f}_{5} = {\left( 5!\right) }^{3} - \left\lbrack {\left( \begin{array}{l} 5 \\ 1 \end{array}\right) \left( \begin{array}{l} 5 \\ 1 \end{array}\right) \cdot {f}_{4} + \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \left( \begin{array}{l} 5 \\ 2 \end{array}\right) \cdot 2! \cdot {f}_{3} + \left( \begin{array}{l} 5 \\ 3 \end{array}\right) \left( \begin{array}{l} 5 \\ 3 \end{array}\right) \cdot 3! \cdot {f}_{2} + 5!}\right\rbrack = {\left( 5!\right) }^{3} - {306},{720} \]
因此,概率为 \( \frac{{306},{720}}{{\left( 5!\right) }^{3}} = {71}/{400} \) ,答案为(D) 471
2021 AMC 10B 试题/第23题
问题
一个边长为8的正方形被涂成白色,除了四个角落各有一个边长为2的黑色等腰直角三角形区域,以及正方形中心有一个边长为 \( 2\sqrt{2} \) 的黑色菱形,如图所示。一枚直径为1的圆形硬币被随机抛到正方形上,且硬币完全落在正方形内。硬币覆盖正方形黑色区域部分的概率可以表示为 \( \frac{1}{196}\left( {a + b\sqrt{2} + \pi }\right) \) ,其中 \( a \) 和 \( b \) 为正整数。 \( a + b \) 是多少?
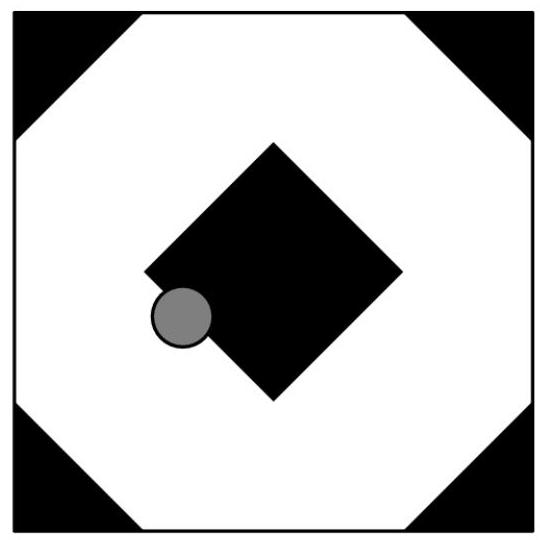
解决方案
为了求出概率,我们考察总可能区域:硬币中心到正方形任一边的距离必须至少为 \( \frac{1}{2} \) ,因为这是硬币的半径。这意味着总可能区域是一个边长为 \( 8 - \frac{1}{2} - \frac{1}{2} = 7 \) 的正方形,面积为49。接下来,我们分情况讨论硬币需要落在哪些位置才能部分覆盖黑色区域。
靠近中心广场
我们可以让硬币的中心落在中心方格 \( \frac{1}{2} \) 的范围内,或者落在中心方格内部。也就是说,硬币中心要么落在方格之外,要么落在方格之内。因此,我们得到一个区域:从方格外部的每一点向外延伸 \( \frac{1}{2} \) 。
形成4个四分之一圆和4个矩形。这4个四分之一圆拼成一个完整圆,半径为 \( \frac{1}{2} \) ,因此其面积为 \( \frac{\pi }{4} \) 。一个矩形的面积为 \( 2\sqrt{2} \cdot \frac{1}{2} = \sqrt{2} \) ,所以4个矩形总面积为 \( 4\sqrt{2} \) 。黑色正方形的面积就是 \( {\left( 2\sqrt{2}\right) }^{2} = 8 \) 。因此,在此情况下,我们得到总面积为 \( 8 + 4\sqrt{2} + \frac{\pi }{4} \) 。接下来进入第二种(也是最后一种)情况。
三角之畔
我们也可以让硬币落在距离某个三角形 \( \frac{1}{2} \) 的范围内。根据对称性,只需计算其中一个三角形的成功区域,再乘以4即可。考虑这个示意图。我们可以从正方形底角向蓝色三角形的斜边作一条高。这条高穿过黑色区域时的长度为 \( \sqrt{2} \) ,而穿过
白色区域(同时位于蓝色三角形内)是 \( \frac{1}{2} \) 。然而,当不穿过红色正方形时,我们必须减去。此时,它是一个边长为 \( \frac{\frac{1}{2}}{\sqrt{2}} \) 的小等腰直角三角形的斜边,即 \( \frac{\sqrt{2}}{2} \) 。因此,蓝色三角形的高为 \( \sqrt{2} + \frac{1}{2} - \frac{\sqrt{2}}{2} = \frac{\sqrt{2} + 1}{2} \) 。然后,回想一下,等腰直角三角形的面积是 \( {h}^{2} \) ,其中 \( h \) 是从直角顶点引出的高。因此,平方后得到 \( \frac{3 + 2\sqrt{2}}{4} \) 。现在,为了考虑所有黑色三角形,我们需要将其乘以4,得到 \( 3 + 2\sqrt{2} \) 作为此情况的最终面积。
完成
然后,为了让硬币接触到黑色区域,我们将成功区域(successful regions)的面积相加,即
\( 8 + 4\sqrt{2} + \frac{\pi }{4} + 3 + 2\sqrt{2} = {11} + 6\sqrt{2} + \frac{\pi }{4} = \frac{{44} + {24}\sqrt{2} + \pi }{4} \) 总面积为49,因此我们的概率为 \( \frac{\frac{{44} + {24}\sqrt{2} + \pi }{4}}{49} = \frac{{44} + {24}\sqrt{2} + \pi }{196} \) ,这意味着 \( a + b = {44} + {24} = {68} \) 。这对应选项(C) 68。~rocketsri
2021 AMC 12B 试题/第22题
以下题目同时出现在2021年AMC 10B第24题和2021年AMC 12B第22题,因此两道题均重定向至此页面。
问题
阿俊和贝丝玩一个游戏,他们轮流从一组砖墙中的一堵“墙”上取走一块砖或两块相邻的砖,取走后留下的空隙可能会形成新的墙。所有墙都只有一块砖高。例如,一堵由4块砖和2块砖组成的墙,经过一步操作后可以变成以下任意一种: \( \left( {3,2}\right) ,\left( {2,1,2}\right) ,\left( 4\right) ,\left( {4,1}\right) ,\left( {2,2}\right) , \) 或 \( \left( {1,1,2}\right) . \)

阿俊先手,移除最后一块砖的人获胜。在哪种初始配置下,贝丝有必胜策略?
(A)(6,1,1) (B)(6,2,1) (C)(6,2,2) (D)(6,3,1) (E)(6,3,2)
解决方案
首先,我们注意到对称局面对于即将行动的玩家是必败的。接着我们开始检查小规模局面。(n) 对先手总是必胜。此外,(3,2,1) 是必败的, \( \left( {4,1}\right) . \) 亦然。我们考察由 \( \left( {6,2,1}\right) , \) 产生的所有局面,因为 (6,1,1) 显然可以通过 \( \left( {2,2,1,1}\right) . \) 取胜。从 (6,2,1) 出发,先手可以走出的不同局面有
\( \left( {2,2,2,1}\right) ,\left( {1,3,2,1}\right) ,\left( {4,2,1}\right) ,\left( {6,1}\right) ,\left( {5,2,1}\right) ,\left( {4,1,2,1}\right) ,\left( {3,2,2,1}\right) . \) 现在我们逐一列出对这些走法的反驳: \( \left( {2,2,2,1}\right) - \left( {2,1,2,1}\right) \) \( \left( {1,3,2,1}\right) - \left( {3,2,1}\right) \) \( \left( {4,2,1}\right) - \left( {4,1}\right) \) \( \left( {6,1}\right) - \left( {4,1}\right) \) \( \left( {5,2,1}\right) - \left( {3,2,1}\right) \) \( \left( {4,1,2,1}\right) - \left( {2,1,2,1}\right) \) \( \left( {3,2,2,1}\right) - \left( {1,2,2,1}\right) \) 这证明了(6,2,1)对先手方是必败局面。——注意:总体而言,这个游戏极为复杂。例如(8,7,5,3,2)对先手方是必胜局面,但要证明这一点可不容易。
解法2(排除法)
(6,1,1)可以被阿俊(Arjun)变成(2,2,1,1),这是对称的,因此贝丝(Beth)会输。
(6,3,1)可被阿俊变为(3,1,3,1),该序列对称,因此贝丝将输。
(6,2,2)可被阿俊变为(2,2,2,2),该序列对称,因此贝丝将输。
(6,3,2)可被阿俊变为(3,2,3,2),该序列对称,因此贝丝将输。
这样就只剩下(6,2,1)或(B)
解法3(尼姆值)
设当某人刚刚移走最后一块砖时的终局尼姆值(Nim-value)为0,则任何尼姆值为0的局面都是必败局面。众所周知,一个超级游戏(由两个或更多独立游戏组合而成)的尼姆值是其组成各独立游戏尼姆值的二进制异或。因此,我们计算长度不超过6的“单墙”状态的尼姆值(因为选项只到6)。
首先,只有1块砖的游戏尼姆值为1。
同理,2块砖的游戏尼姆值为2。
接下来考虑3块砖的墙。下一步后可能得到的局面为:1块砖、2块砖的墙,或2块独立的砖。前两种的尼姆值分别为1和2,最后一种的尼姆值为 \( 1 \oplus 1 = 0 \) ,因此该状态的尼姆值为3。
再看4块砖的墙。可能的局面有:2块砖的墙、3块砖的墙、2块砖的墙加1块砖的墙,或1块砖的墙加1块砖的墙。这些状态的尼姆值分别为2、3、3和0,因此该状态的尼姆值为1。
[为什么它的尼姆值是1?——awesomediabrine
https://en.wikipedia.org/wiki/Mex_(mathematics)]
5块砖的墙下一步后可能的局面如下:3块砖的墙、4块砖的墙、3块砖的墙加1块砖的墙、两个2块砖的墙,以及2块砖的墙加1块砖的墙。它们的尼姆值分别为3、1、2、0和3,因此5块砖的墙的尼姆值为4。
最后,我们求6块砖的墙的尼姆值。可能的局面有:5块砖的墙、4块砖的墙加1块砖的墙、3块砖的墙加2块砖的墙、4块砖的墙、3块砖的墙加1块砖的墙,以及两个2块砖的墙。这些局面的尼姆值分别为4、0、1、1、2和0,因此6块砖的墙的尼姆值为3。
题目问哪个选项是必败的,即尼姆值为0。我们看到选项 \( \mathbf{\left( A\right) } \) 的尼姆值为 \( 3 \oplus 1 \oplus 1 = 3 \) ,选项(B)的尼姆值为 \( 3 \oplus 2 \oplus 1 = 0 \) ,选项(C)的尼姆值为 \( 3 \oplus 2 \oplus 2 = 3 \) ,选项 \( \mathbf{\left( D\right) } \) 的尼姆值为 \( 3 \oplus 3 \oplus 1 = 1 \) ,选项 \( \mathbf{\left( E\right) } \) 的尼姆值为 \( 3 \oplus 3 \oplus 2 = 2 \) ,所以答案是(B)(6,2,1)
该方法也可推广到解决第一个解法后的附注。用同样方法可得7块砖的墙和8块砖的墙的尼姆值分别为2和1,因此(8,7,5,3,2)的尼姆值为 \( 1 \oplus 2 \oplus 4 \oplus 3 \oplus 2 = 6 \) ,是必胜局面。
2021 AMC 12B 第25题
以下题目同时出现在2021 AMC 10B第25题和2021 AMC 12B第25题,因此两题均重定向至此页。
题目
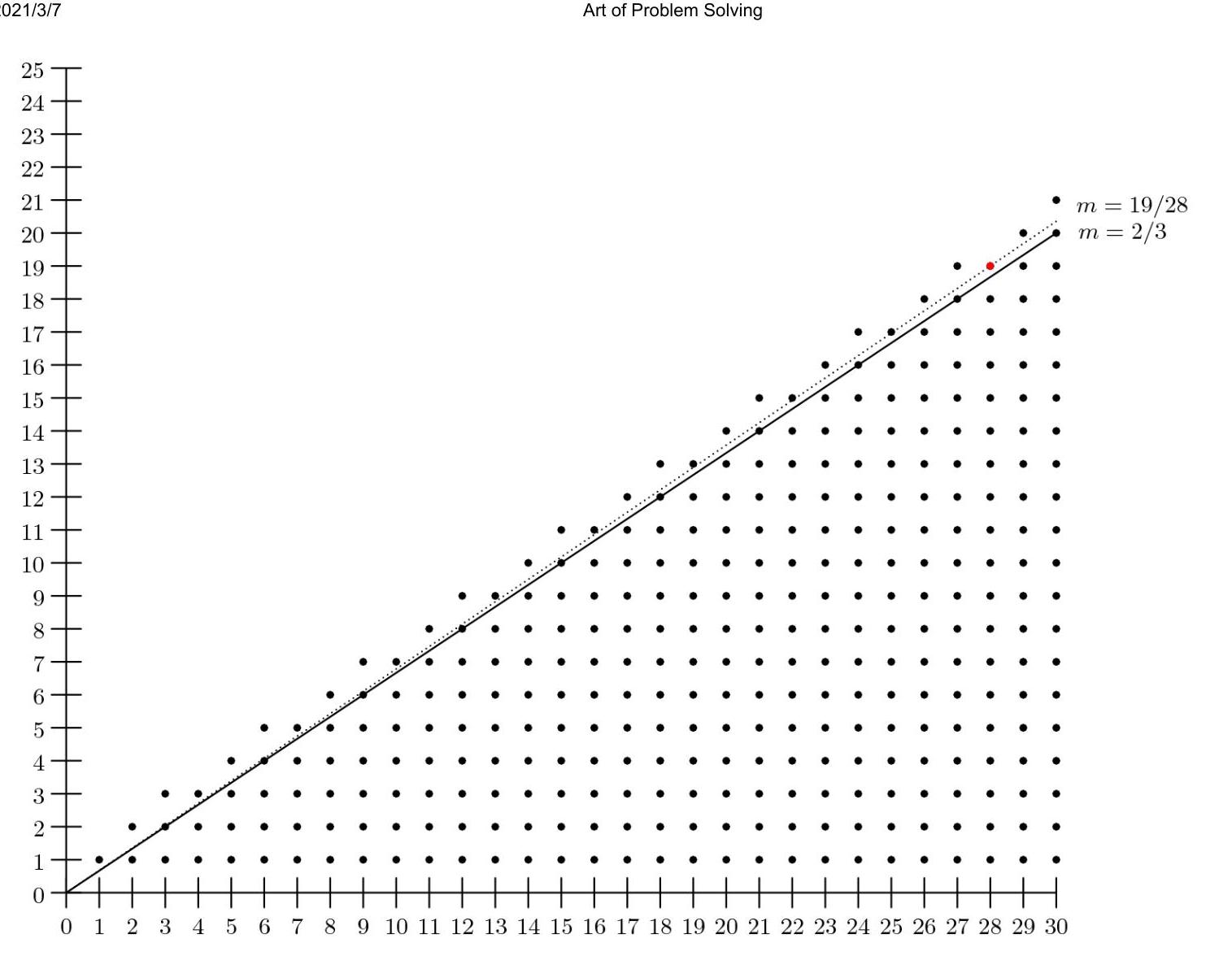
设 \( S \) 为坐标平面上所有格点(坐标均为1到30的整数)的集合。恰有300个 \( S \) 中的点位于或低于方程为 \( y = {mx} \) 的直线。则 \( m \) 的可能值位于一个长度为 \( \frac{a}{b} \) 的区间,其中 \( a \) 与 \( b \) 为互质的正整数。求 \( a + b \) 。
(A) 31 (B) 47 (C) 62 (D) 72 (E) 85
解法1
首先,我们给 \( S \) 中位于直线 \( y = {mx}. \) 下方的格点数量找一个数值表示。对于任意 \( x, \) ,直线 \( y = {mx} \) 下方最高的格点是 \( \lfloor {mx}\rfloor \) 。由于从(x,1)到 \( \left( {x,\lfloor {mx}\rfloor }\right) \) 的所有格点都在直线下方,直线下方的格点总数为 \( \mathop{\sum }\limits_{{x = 1}}^{{30}}\left( {\lfloor {mx}\rfloor }\right) \) 。
接下来,我们为 \( m. \) 寻找下界和上界。为求下界,先作近似:若直线下方有300个格点,则 \( \frac{1}{3} \) 所围区域中约 \( S \) 的面积位于直线下方。利用三角形面积公式,当 \( x = {30}, y \approx {20} \) 时,可解得 \( m \) 。假设(30,20)在直线上,解得 \( m = \frac{2}{3} \) 。将 \( m \) 代入 \( \mathop{\sum }\limits_{{x = 1}}^{{30}}\left( {\lfloor {mx}\rfloor }\right) \) ,得到:
\[ \mathop{\sum }\limits_{{x = 1}}^{{30}}\left( \left\lfloor {\frac{2}{3}x}\right\rfloor \right) = 0 + 1 + 2 + 2 + 3 + \cdots + {18} + {18} + {19} + {20} \]
每3个值出现一次重复(每当 \( y = \frac{2}{3}x \) 经过一个格点时)。因此,可用等差数列计算上述值:
\[ \mathop{\sum }\limits_{{x = 1}}^{{30}}\left( \left\lfloor {\frac{2}{3}x}\right\rfloor \right) = 0 + 1 + 2 + 2 + 3 + \cdots + {18} + {18} + {19} + {20} \]
\[ = \frac{{20}\left( {21}\right) }{2} + 2 + 4 + 6 + \cdots + {18} \]
\[ = {210} + \frac{20}{2} \cdot 9 \]
\[ = {300} \]
这意味着 \( \frac{2}{3} \) 是 \( m. \) 的一个可能值,并且是 \( m. \) 的下界。原因在于 \( y = \frac{2}{3}x \) 穿过许多点(如(21,14))。若 \( m \) 再小, \( y = \frac{2}{3}x \) 将不再穿过其中某些点,直线下方将不足300个格点。2021/3/7 现在求 \( m. \) 的上界:想象缓慢增大 \( m \) ,并从 \( m = \frac{2}{3} \) 的下界开始旋转直线 \( y = {mx}, \) 。 \( m \) 的上界出现在 \( y = {mx} \) 再次穿过一个格点时(可参考此题以更好理解:https://artofproblemsolving.com/wiki/index.php/2011_AMC_10B_Problems/Problem_24)。
换言之,我们寻找第一个可表示为 \( \frac{p}{q} \) 正整数比值的 \( m > \frac{2}{3} \) ,其中 \( q \leq {30} \) 。对每个 \( q = 1,\ldots ,{30} \) , \( \frac{1}{q} \) 超过 \( \frac{2}{3} \) 的最小倍数分别为 \( 1,\frac{2}{2},\frac{3}{3},\frac{3}{4},\frac{4}{5},\cdots ,\frac{19}{27},\frac{19}{28},\frac{20}{29},\frac{21}{30} \) ,其中最小的是 \( \frac{19}{28} \) 。注意:从 \( \frac{21}{30} \) 开始列出 \( \frac{1}{q} \) 的倍数,会发现它们离 \( \frac{2}{3} \) 越来越远。另见解法2中找上界的方法。下界为 \( \frac{2}{3} \) ,上界为 \( \frac{19}{28} \) ,二者之差为 \( \frac{1}{84} \) ,故答案为 \( 1 + {84} = {85} \) ~JimY
解法2
我知道我希望直线 \( \frac{2}{3} \) 上方的整数坐标盒子中约有 \( \frac{2}{3} \) 的部分。每个轴在所需范围内共有30个整数坐标,因此总共有900个格点。我估计斜率为 \( \frac{2}{3} \) 。现在,尽管可能存在更简单的解法,我会尝试统计直线上方的点数,看看是否有600个点位于直线上方。直线将盒子内部区域划分,使得 \( \frac{2}{3} \) 的区域位于直线上方。
我发现当 \( x = 1 \) 时,直线上方的坐标数为30;当时,直线上方的坐标数为29。每当直线穿过一个具有整数坐标的y值时,直线上方的点数就会减少1。我写出了30项的和,希望能找到规律。我绘制了前几个正整数x坐标,发现直线上方的整数之和为。偶数在每三个项中重复一次。我发现每一项的平均值为20,共有30项,这意味着直线上方恰好有600个点,符合预期。这给出了下界,因为如果斜率稍微减小,直线穿过的点将位于直线上方。
为了找到上界,请注意每个具有整数x坐标的点要么 \( \frac{1}{3} \) 要么位于直线上方。由于通过某点的斜率为y坐标除以x坐标,斜率的微小变化会增加较高x坐标对应的y值。我们将注意力转向,直线与之相交于。点(30,20)已被计入直线下方,我们可以清楚地看到,如果缓慢增加直线的斜率,我们将经过点(28,19),因为更接近格点。通过原点与(28,19)的直线斜率为。这给出了上界。
取上界 \( \mathrm{m} \) 并减去下界,得到。这就是答案。(E)85。~theAJL图示
解法3
另一种采用与解法1相同方法论的途径是使用皮克定理(Pick's Theorem)。维基百科页面:https://en.wikipedia.org/wiki/Pick%27s_theorem 这是一个用于计算多边形内部严格格点数量的公式。下界的近似仍然是必要的。